| | An arc of a circle is a "portion" of the circumference of the circle. The length of an arc is only the length of its "portion" of the circumference. The circumference itself can be considered a full circle arc length. | 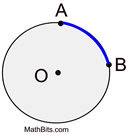 | |  | Arc Mensurate: In a circumvolve, the degree measure of an arc is equal to the measure out of the cardinal angle that intercepts the arc. | |  | Arc Length: In a circle, the length of an arc is a portion of the circumference. The letter of the alphabet "s" is used to represent arc length. | | 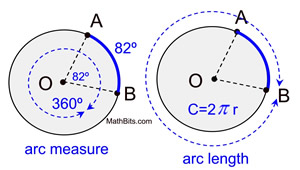 | Consider the following proportion: 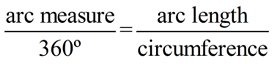 | If we solve the proportion for arc length, and supplant "arc measure"
with its equivalent "key bending", we tin can establish the formula: 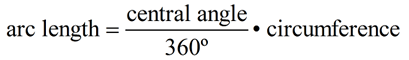 Discover that arc length is a partial part of the circumference. For case, an arc mensurate of 60º is one-sixth of the circle (360º), so the length of that arc will exist one-sixth of the circumference of the circle. 
In circle O, the radius is 8 inches and minor arc 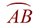 is intercepted by a cardinal bending of 110 degrees. Find the length of minor arc is intercepted by a cardinal bending of 110 degrees. Find the length of minor arc 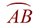 to the nearest integer. to the nearest integer.

As you lot progress in your report of mathematics and angles, you lot will encounter more than references fabricated to the term "radians" instead of "degrees". And then, what is a "radian" ? |  | The radian measure, θ, of a central bending is defined equally the ratio of the length of the arc | | the angle subtends, southward , divided by the radius of the circle, r. | which gives arc length, south : southward = θr | 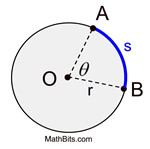
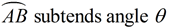
subtend = "to be opposite to" | | One radian is the cardinal angle that subtends an arc length of ane radius ( s = r).
Since all circles are similar, one radian is the same value for all circles. |  Human relationship betwixt Degrees and Radians:
In a circle, the arc measure of the entire circumvolve is 360º and the arc length of the unabridged circle is represented past the formula for circumference of the circle:  . . Substituting C into the formula s = θr shows:
C = θr2 πr = θr 2 π = θ
The arc measure of the cardinal bending of an entire circle is 360º and the radian measure of the cardinal angle of an entire circumvolve = twoπ.
360º (degrees) = 2π (radians)
| 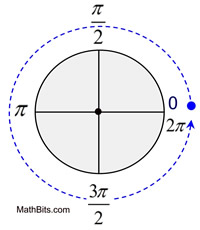 | | 360º = twoπ
(divide both sides by 2)
180º = π | 360º = twoπ
(divide both sides by 4)
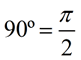 | 360º = 2π
(divide both sides past 360)
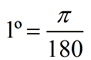
| 360º = 2π
(divide both sides by iiπ)
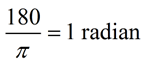
| 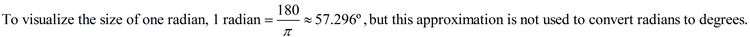 To change
from degrees to radians,
multiply degrees past  | To alter
from radians to degrees,
multiply radians by 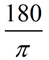 | Justify why: The length of the arc intercepted past a fundamental angle is proportional to the radius. | The diagram at the correct shows two circles with the same center (concentric circles). It has already been shown that concentric circles are like under a dilation transformation. The ratio of similitude of the smaller circle to the larger circle is:
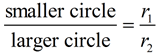 | 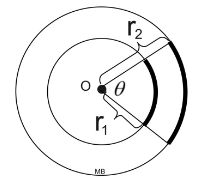 | | The aforementioned dilation that mapped the smaller circle onto the larger circle will also map the piece (sector) of the smaller circle with an arc length of due south one onto the slice (sector) of the larger circle with an arc length of southward 2. When the radius gets dilated by a scale factor, the arc length is also dilated by that same scale gene. | 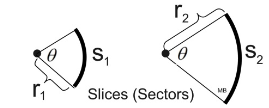 Equally long as the fundamental angles are the same, the slices (sectors) volition be similar. Equally long as the fundamental angles are the same, the slices (sectors) volition be similar. | Since corresponding parts of like figures are in proportion, 
An equivalent proportion can be written as 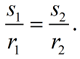 This proportion shows that the ratio of the arc length intercepted by a cardinal angle to the radius of the circle volition always yield the same (constant) ratio. This proportion shows that the ratio of the arc length intercepted by a cardinal angle to the radius of the circle volition always yield the same (constant) ratio. In relation to the two arc length formulas seen on this page, both evidence that arc length, southward, is expressed as "some value" times the radius, r. The arc length is proportional to the radius. When θ is in degrees:  | When θ is in radians: 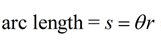 | Setting r = ane shows the constant of proportionality.

Annotation: The re-posting of materials (in part or whole) from this site to the Internet is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". | |

Source: https://mathbitsnotebook.com/Geometry/Circles/CRArcLengthRadian.html
Posted by: wigginscolusay.blogspot.com



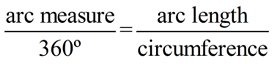
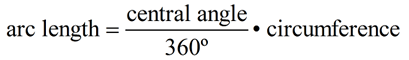



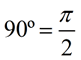
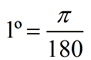
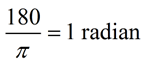

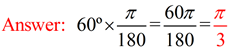
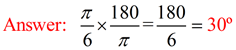

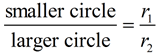

 Equally long as the fundamental angles are the same, the slices (sectors) volition be similar.
Equally long as the fundamental angles are the same, the slices (sectors) volition be similar. 
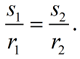 This proportion shows that the ratio of the arc length intercepted by a cardinal angle to the radius of the circle volition always yield the same (constant) ratio.
This proportion shows that the ratio of the arc length intercepted by a cardinal angle to the radius of the circle volition always yield the same (constant) ratio.

0 Response to "How To Find Arc Length With Radians"
Post a Comment