How to Find if Triangles are Similar

2 triangles are similar if they have:

  • all their angles equal
  • corresponding sides are in the same ratio

But we don't need to know all iii sides and all three angles ...two or three out of the six is usually enough.

At that place are three ways to find if ii triangles are similar: AA, SAS and SSS:

AA

AA stands for "angle, angle" and means that the triangles have two of their angles equal.

If two triangles have two of their angles equal, the triangles are similar.

Example: these 2 triangles are similar:

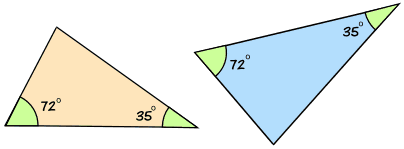
triangles similar both have angles 72 and 35

If two of their angles are equal, then the third angle must also be equal, because angles of a triangle always add together to brand 180°.

In this case the missing angle is 180° − (72° + 35°) = 73°

So AA could also be called AAA (because when two angles are equal, all three angles must be equal).

SAS

SAS stands for "side, angle, side" and means that nosotros have two triangles where:

  • the ratio between 2 sides is the same as the ratio between another two sides
  • and we we likewise know the included angles are equal.

If two triangles have two pairs of sides in the same ratio and the included angles are besides equal, then the triangles are similar.

Example:

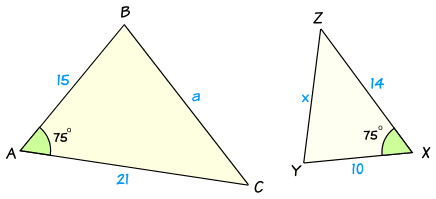
triangles similar both have angle 75 but sides (15,21,a) and (10,14,x)

In this example we can come across that:

  • 1 pair of sides is in the ratio of 21 : 14 = 3 : ii
  • some other pair of sides is in the ratio of 15 : 10 = 3 : 2
  • in that location is a matching angle of 75° in between them

And so at that place is enough information to tell us that the ii triangles are similar.

Using Trigonometry

We could also utilize Trigonometry to calculate the other ii sides using the Law of Cosines:

Example Continued

In Triangle ABC:

  • a2 = b2 + cii - 2bc cos A
  • a2 = 21two + 15two - 2 × 21 × xv × Cos75°
  • atwo = 441 + 225 - 630 × 0.2588...
  • a2 = 666 - 163.055...
  • a2 = 502.944...
  • So a = √502.94 = 22.426...

In Triangle XYZ:

  • xtwo = yii + zii - 2yz cos X
  • x2 = xivtwo + ten2 - ii × 14 × x × Cos75°
  • ten2 = 196 + 100 - 280 × 0.2588...
  • x2 = 296 - 72.469...
  • ten2 = 223.530...
  • So x = √223.530... = xiv.950...

Now let united states check the ratio of those 2 sides:

a : x = 22.426... : 14.950... = three : 2

the aforementioned ratio equally before!

Annotation: we tin also use the Law of Sines to show that the other two angles are equal.

SSS

SSS stands for "side, side, side" and means that we have two triangles with all iii pairs of corresponding sides in the same ratio.

If ii triangles have three pairs of sides in the same ratio, and then the triangles are similar.

Instance:

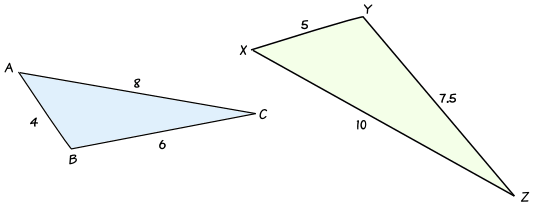
triangles (4,6,8) and (5,7.5,10)

In this example, the ratios of sides are:

  • a : ten = 6 : 7.v = 12 : fifteen = 4 : v
  • b : y = 8 : 10 = 4 : 5
  • c : z = iv : 5

These ratios are all equal, and then the ii triangles are similar.

Using Trigonometry

Using Trigonometry we can show that the two triangles take equal angles by using the Law of Cosines in each triangle:

In Triangle ABC:

  • cos A = (btwo + c2 - a2)/2bc
  • cos A = (82 + 42 - vi2)/(two× eight × 4)
  • cos A = (64 + sixteen - 36)/64
  • cos A = 44/64
  • cos A = 0.6875
  • So Angle A = 46.6°

In Triangle XYZ:

  • cos X = (yii + zii - xii)/2yz
  • cos X = (102 + 5ii - 7.v2)/(2× ten × 5)
  • cos 10 = (100 + 25 - 56.25)/100
  • cos 10 = 68.75/100
  • cos X = 0.6875
  • So Angle X = 46.6°

So angles A and X are equal!

Similarly nosotros tin can show that angles B and Y are equal, and angles C and Z are equal.