how to find the intercepts of a graph
Graphs
70 Graphing with Intercepts
Learning Objectives
By the terminate of this section, you volition exist able to:
- Identify the intercepts on a graph
- Find the intercepts from an equation of a line
- Graph a line using the intercepts
- Choose the most convenient method to graph a line
Place the Intercepts on a Graph
Every linear equation has a unique line that represents all the solutions of the equation. When graphing a line past plotting points, each person who graphs the line tin cull any 3 points, so two people graphing the line might use dissimilar sets of points.
At first glance, their 2 lines might appear unlike since they would have dissimilar points labeled. Just if all the work was done correctly, the lines will be exactly the same line. 1 way to recognize that they are indeed the aforementioned line is to focus on where the line crosses the axes. Each of these points is chosen an intercept of the line.
Intercepts of a Line
Each of the points at which a line crosses the ![]() and the
and the ![]() is called an intercept of the line.
is called an intercept of the line.
Let's wait at the graph of the lines shown in (Figure).
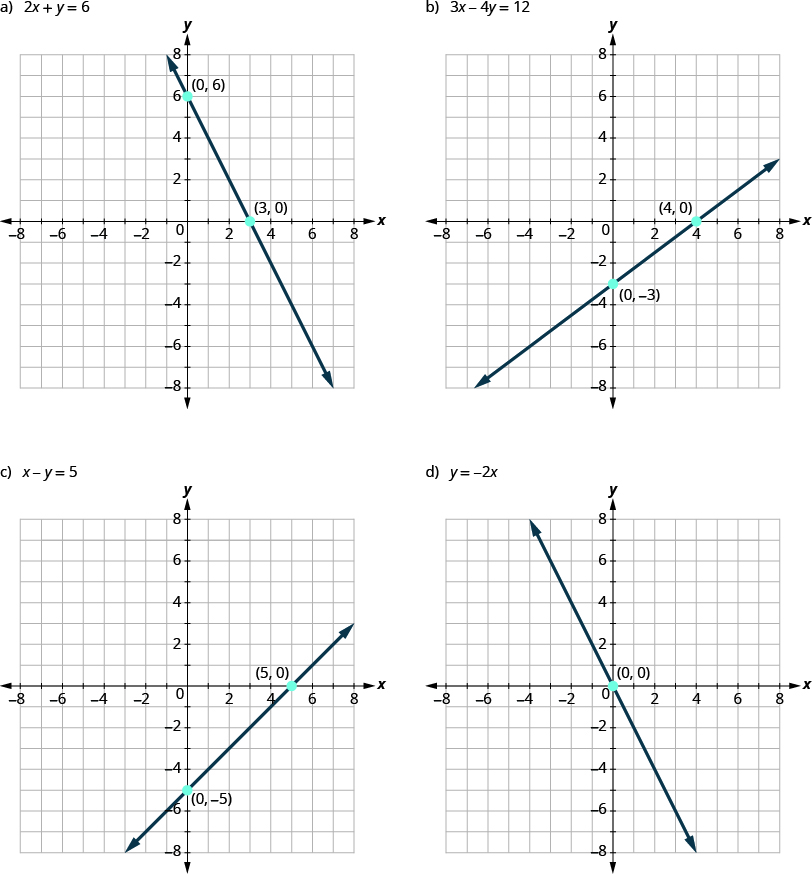
First, notice where each of these lines crosses the x– axis:
| Figure: | The line crosses the ten-centrality at: | Ordered pair of this point |
|---|---|---|
| 42 | 3 | (3,0) |
| 43 | 4 | (4,0) |
| 44 | 5 | (five,0) |
| 45 | 0 | (0,0) |
Practice you see a pattern?
For each row, the y- coordinate of the point where the line crosses the 10- centrality is cypher. The signal where the line crosses the 10- centrality has the form ![]() ; and is chosen the 10-intercept of the line. The x- intercept occurs when y is zero.
; and is chosen the 10-intercept of the line. The x- intercept occurs when y is zero.
Now, let'south await at the points where these lines cross the y-axis.
| Figure: | The line crosses the y-axis at: | Ordered pair for this bespeak |
|---|---|---|
| 42 | 6 | (0,6) |
| 43 | -3 | (0,-3) |
| 44 | -v | (0,-5) |
| 45 | 0 | (0,0) |
Solution
| ⓐ | |
| The graph crosses the ten-axis at the point (4, 0). | The x-intercept is (4, 0). |
| The graph crosses the y-axis at the betoken (0, 2). | The 10-intercept is (0, 2). |
| ⓑ | |
| The graph crosses the ten-axis at the signal (2, 0). | The x-intercept is (ii, 0) |
| The graph crosses the y-axis at the point (0, −6). | The y-intercept is (0, −6). |
| ⓒ | |
| The graph crosses the x-centrality at the betoken (−5, 0). | The x-intercept is (−5, 0). |
| The graph crosses the y-axis at the point (0, −v). | The y-intercept is (0, −5). |
Find the ![]() and
and ![]() of the graph:
of the graph: ![]()
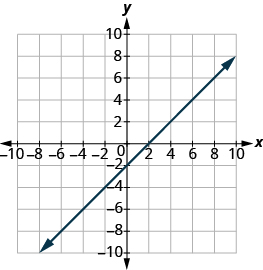
x-intercept (2,0): y-intercept (0,−2)
Find the ![]() and
and ![]() of the graph:
of the graph: ![]()
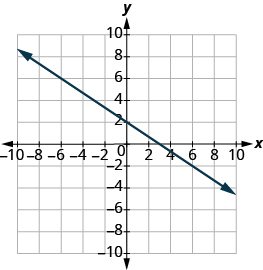
x-intercept (3,0); y-intercept (0,2)
Find the Intercepts from an Equation of a Line
Recognizing that the ![]() occurs when
occurs when ![]() is zero and that the
is zero and that the ![]() occurs when
occurs when ![]() is zero gives us a method to find the intercepts of a line from its equation. To observe the
is zero gives us a method to find the intercepts of a line from its equation. To observe the ![]() allow
allow ![]() and solve for
and solve for ![]() To find the
To find the ![]() let
let ![]() and solve for
and solve for ![]()
Discover the ten and y from the Equation of a Line
Use the equation to discover:
| ten | y |
|---|---|
| 0 | |
| 0 |
Find the intercepts of ![]()
Find the intercepts of ![]()
Detect the intercepts of the line: ![]()
x-intercept (4,0); y-intercept: (0,−3)
Discover the intercepts of the line: ![]()
x-intercept (4,0); y-intercept: (0,−2)
Graph a Line Using the Intercepts
To graph a linear equation by plotting points, you can use the intercepts as ii of your iii points. Detect the two intercepts, and and then a third point to ensure accuracy, and depict the line. This method is often the quickest mode to graph a line.
Graph ![]() using intercepts.
using intercepts.
Solution
First, observe the ![]() Let
Let ![]()
The ![]() is
is ![]()
At present discover the ![]() Let
Let ![]()
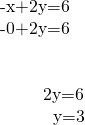
The ![]() is
is ![]()
Notice a third point. We'll use ![]()
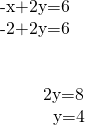
A third solution to the equation is ![]()
Summarize the three points in a table and then plot them on a graph.
| | ||
|---|---|---|
| ten | y | (x,y) |
| | | |
| | | |
| | | |
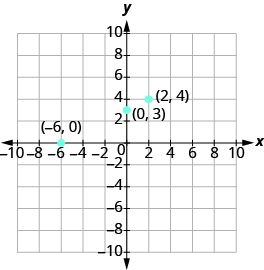
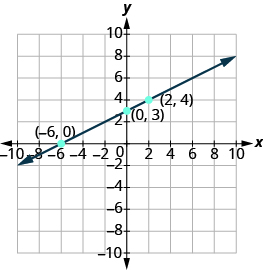
Do the points line upward? Aye, so draw line through the points.
Graph the line using the intercepts: ![]()
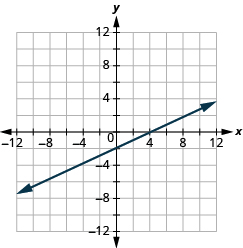
Graph the line using the intercepts: ![]()
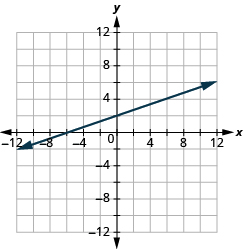
Graph a line using the intercepts.
- Find the
 and
and  of the line.
of the line. - Notice a third solution to the equation.
- Plot the iii points then bank check that they line up.
- Draw the line.
Graph ![]() using intercepts.
using intercepts.
Graph the line using the intercepts: ![]()
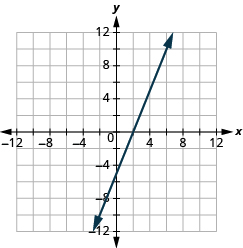
Graph the line using the intercepts: ![]()
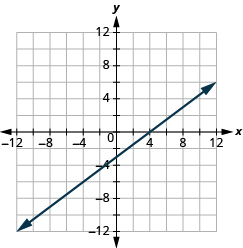
Graph ![]() using the intercepts.
using the intercepts.
Graph using the intercepts: ![]()
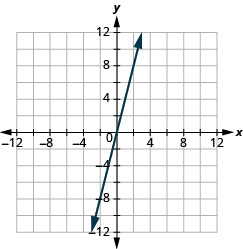
Graph using the intercepts: ![]()
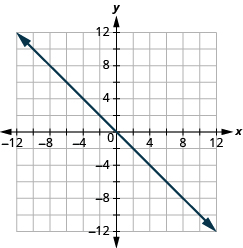
Choose the Nigh Convenient Method to Graph a Line
While nosotros could graph any linear equation past plotting points, it may non always exist the most convenient method. This table shows six of equations nosotros've graphed in this chapter, and the methods we used to graph them.
| Equation | Method | |
|---|---|---|
| #1 | | Plotting points |
| #2 | | Plotting points |
| #three | | Vertical line |
| #iv | | Horizontal line |
| #5 | | Intercepts |
| #six | | Intercepts |
What is it almost the form of equation that tin can help us choose the most convenient method to graph its line?
Notice that in equations #i and #2, y is isolated on one side of the equation, and its coefficient is i. We found points by substituting values for x on the correct side of the equation and then simplifying to get the corresponding y- values.
Equations #three and #4 each take just one variable. Retrieve, in this kind of equation the value of that one variable is constant; it does non depend on the value of the other variable. Equations of this form accept graphs that are vertical or horizontal lines.
In equations #five and #vi, both x and y are on the aforementioned side of the equation. These two equations are of the grade ![]() . We substituted
. We substituted ![]() and
and ![]() to notice the x- and y- intercepts, and then found a tertiary point past choosing a value for ten or y.
to notice the x- and y- intercepts, and then found a tertiary point past choosing a value for ten or y.
This leads to the post-obit strategy for choosing the almost user-friendly method to graph a line.
Choose the nigh convenient method to graph a line.
- If the equation has only i variable. It is a vertical or horizontal line.
- If
 is isolated on one side of the equation. Graph past plotting points.
is isolated on one side of the equation. Graph past plotting points. - If the equation is of the form
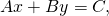 discover the intercepts.
discover the intercepts.
Solution
ⓐ ![]()
This equation has simply one variable, ![]() Its graph is a horizontal line crossing the
Its graph is a horizontal line crossing the ![]() at
at ![]()
ⓑ ![]()
This equation is of the course ![]() Find the intercepts and one more point.
Find the intercepts and one more point.
ⓒ ![]()
In that location is only one variable, ![]() The graph is a vertical line crossing the
The graph is a vertical line crossing the ![]() at
at ![]()
ⓓ ![]()
Since ![]() is isolated on the left side of the equation, information technology volition be easiest to graph this line by plotting iii points.
is isolated on the left side of the equation, information technology volition be easiest to graph this line by plotting iii points.
- ⓐ intercepts
- ⓑ horizontal line
- ⓒ plotting points
- ⓓ vertical line
- ⓐ vertical line
- ⓑ plotting points
- ⓒ horizontal line
- ⓓ intercepts
Key Concepts
Practice Makes Perfect
Identify the Intercepts on a Graph
In the following exercises, find the ![]() and
and ![]() intercepts.
intercepts.
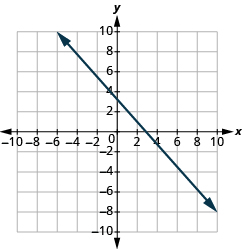
(3,0),(0,three)
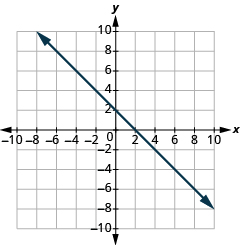
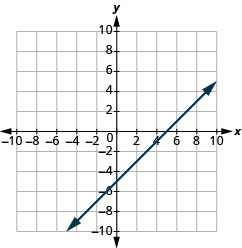
(5,0),(0,−5)
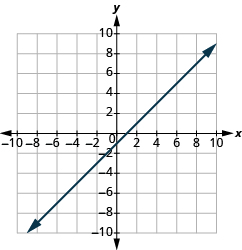
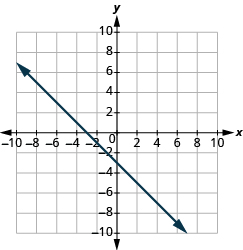
(−2,0),(0,−2)
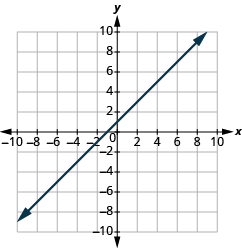
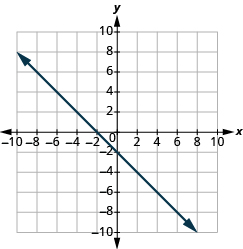
(−i,0),(0,one)
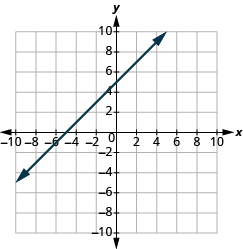
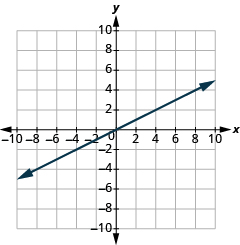
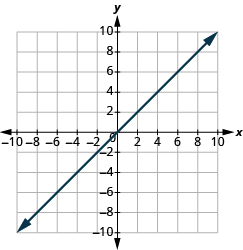
(0,0)
Detect the ![]() and
and ![]() Intercepts from an Equation of a Line
Intercepts from an Equation of a Line
In the following exercises, find the intercepts.
![]()
(4,0),(0,iv)
![]()
![]()
(−two,0),(0,−2)
![]()
![]()
(v,0),(0,−5)
![]()
![]()
(−3,0),(0,3)
![]()
![]()
(8,0),(0,four)
![]()
![]()
(2,0),(0,6)
![]()
![]()
(12,0),(0,−iv)
![]()
![]()
(2,0),(0,−8)
![]()
![]()
(5,0),(0,2)
![]()
![]()
(4,0),(0,−six)
![]()
![]()
(3,0),(0,−1)
![]()
![]()
(−10,0),(0,2)
![]()
![]()
(0,0)
![]()
![]()
(0,0)
![]()
Graph a Line Using the Intercepts
In the following exercises, graph using the intercepts.
![]()
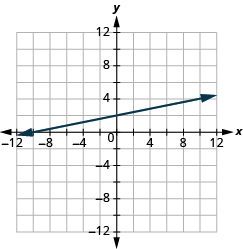
![]()
![]()
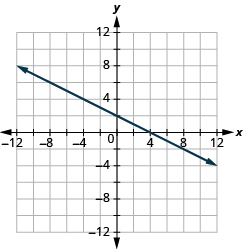
![]()
![]()
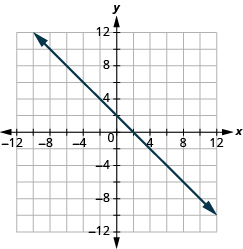
![]()
![]()
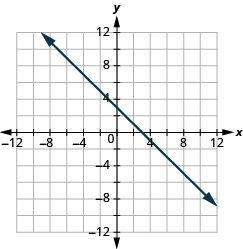
![]()
![]()
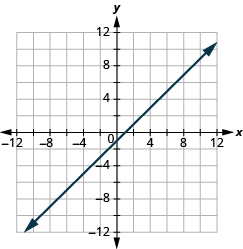
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Choose the Most Convenient Method to Graph a Line
In the post-obit exercises, identify the near user-friendly method to graph each line.
![]()
vertical line
![]()
![]()
horizontal line
![]()
![]()
plotting points
![]()
![]()
intercepts
![]()
![]()
plotting points
![]()
![]()
horizontal line
![]()
![]()
intercepts
![]()
![]()
plotting points
![]()
Everyday Math
Road trip Damien is driving from Chicago to Denver, a altitude of ![]() miles. The
miles. The ![]() on the graph below shows the time in hours since Damien left Chicago. The
on the graph below shows the time in hours since Damien left Chicago. The ![]() represents the distance he has left to drive.
represents the distance he has left to drive.
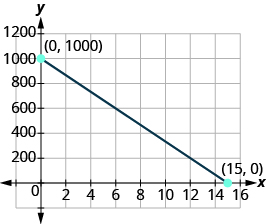
ⓐ Find the ![]() and
and ![]() intercepts
intercepts
ⓑ Explicate what the ![]() and
and ![]() intercepts mean for Damien.
intercepts mean for Damien.
ⓐ (0,one,000),(15,0). ⓑ At (0,1,000) he left Chicago 0 hours ago and has 1,000 miles left to drive. At (15,0) he left Chicago fifteen hours ago and has 0 miles left to bulldoze.
Road trip Ozzie filled up the gas tank of his truck and went on a road trip. The ![]() on the graph shows the number of miles Ozzie drove since filling up. The
on the graph shows the number of miles Ozzie drove since filling up. The ![]() represents the number of gallons of gas in the truck'south gas tank.
represents the number of gallons of gas in the truck'south gas tank.
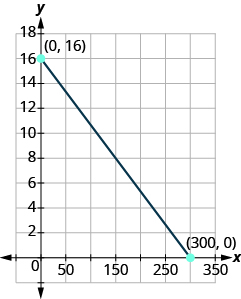
ⓐ Discover the ![]() and
and ![]() intercepts.
intercepts.
ⓑ Explain what the ![]() and
and ![]() intercepts mean for Ozzie.
intercepts mean for Ozzie.
Writing Exercises
How practise you find the ![]() of the graph of
of the graph of ![]()
Answers will vary.
How do yous find the ![]() of the graph of
of the graph of ![]()
Do yous prefer to graph the equation ![]() past plotting points or intercepts? Why?
past plotting points or intercepts? Why?
Answers will vary.
Do you adopt to graph the equation ![]() past plotting points or intercepts? Why?
past plotting points or intercepts? Why?
Self Check
ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this department.
ⓑ What does this checklist tell y'all about your mastery of this section? What steps will yous take to ameliorate?
Glossary
- intercepts of a line
- Each of the points at which a line crosses the x-axis and the y-axis is called an intercept of the line.
Source: https://opentextbc.ca/prealgebraopenstax/chapter/graphing-with-intercepts/
Posted by: wigginscolusay.blogspot.com

0 Response to "how to find the intercepts of a graph"
Post a Comment